决策树
决策树的最优分支选择
分类树
- 枚举所有可能的划分,每次计算一个代价值,取代价最低的分裂方法。
- 设定一个阈值,若超过,则分裂。
回归树
- 在一次分裂时,遍历所有划分方法(每次划分为两组,分别计算损失函数并相加),找出损失函数和最小的作为本次分裂;然后使用递归划分出所有可能。
- 预测时,使用分组的组内平均数作为该组所有元素的预测值;损失函数可以用该组的各值与该组的平均数的残差平方和。
普通回归树的训练过程
- 对回归树结果的不太恰当的通俗理解:在一个局部范围内用平均值来预测这个局部内的所有点的值。
- 回归树的训练过程是一个递归的过程,首先,从分析一个递归环节开始:
- 随机选取一个特征
- 先找到对这个特征的各个二划分点
- 分别对每个划分点作如下计算: 因为每组的预测值为平均数,第i个分组(一共两个分组)的损失函数L(i)为: \[ L(i)=\sum_{j=0}^{1}{(y_i^{(j)}-mean_i)^2} \] 其中,\(j\)为对第i组中每个数的遍历序数,\(mean_i\)为第i组的平均数 整个树在此划分下的损失函数为: \[ L=\sum_i{L(i)} \]
- 比较所有划分,在回归树本次分裂时,取\(L\)最小的划分点作为本次划分点,完成一次递归。
- 经过n次递归达到给定的要求时,回归树停止分裂。
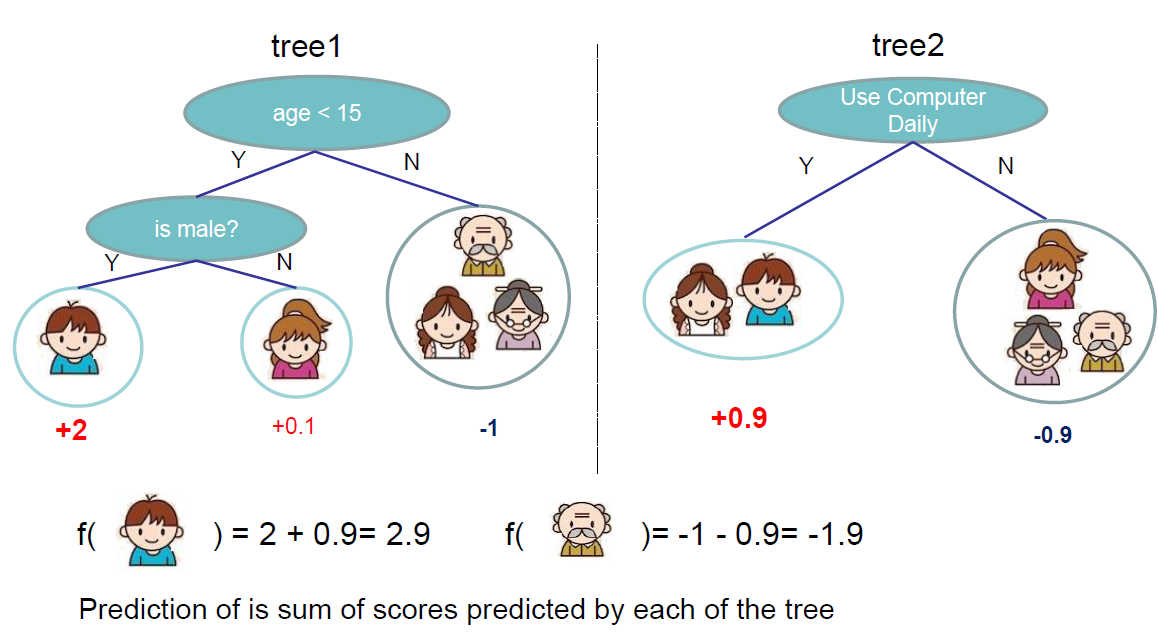
集成树
- 集成树是树模型的一大类模型(boost模型),采用各个树的预测值相加作为预测结果的计算方法进行预测。
AdaBoost
一些特征:
1. 首先,AdaBoost是一种二分类算法。
2. 加性模型,使用前向分步算法作为各个数学公式的来源和依据(即公式为啥长这样)。
3. 从训练数据中学习一系列弱分类器或基本分类器,然后将这些弱分类器组合成一个强分类器
4. 通俗理解思想:增大被分错的数据的权重,减小错误率高的弱分类器的作用。整个学习过程就像是先粗略的对整个数据集进行划分(在递归中的第一个分类器),然后对剩下的分错的数据集抽出来重点对待再次划分(递归中的第二个分类器);通过两种权重的组合(数据权重和弱分类器权重)作用巧妙地得出最终的分类器。这个思想和泰勒展开有着异曲同工之妙,即先大概分,再细分;先整体符合,再对细节下手。
5. 关键:1、如何更新数据的权重。2、如何组合弱分类器(分类器权重)。
整个函数的目的是将\(X\)映射到\(\{-1,1\}\),即求函数:\(G_m(x)→\{-1,1\}\)
- 整个过程:
- 权值初始化,所有权值最开始时都被赋予相同的值: \[
\frac{1}{N}
\] 其中,N是总弱学习器的个数。
- 构建弱分类器
使用具有权值分布\(D_m\)的训练数据集学习,得到基本分类器(具体过程:穷举每个阈值,使用公式计算误差\(e_m\)(公式见后文)选取让误差最低的阈值来设计基本分类器,即一个简单的二分类器) - 计算弱分类器权重:思想为根据错误率调整权重的大小,错误率越大,权值越小。整个权值更新过程如下: 首先,计算中间系数\(α_m\),公式为: \[ α_m=\frac{1}{2}ln\frac{1-e_m}{e_m} \]
- \(e_m\)为误差,计算公式为: \[ e_m=P(G_m(x_i)≠y_i)=\sum_{i=1}^{N}w_{mi}I(G_m(x_i)≠y_i) \]
- \(w_{mi}\)为当前的权重。
- \(I\)为指示函数,代表的是指示函数(indicator function)。 它的含义是:当输入为True的时候,输出为1,输入为False的时候,输出为0。 然后,更新数据权重,过程为: \[
D_{m+1}=(w_{m+1,1},...,w_{m+1,i},...,w_{m+1,N})
\] \[
w_{m+1,i}=\frac{w_{mi}}{Z_m}e^{-α_my_iG_m(x_i)},i=1,2,...,N
\] 其中,\(Z_m\)的计算过程: \[
Z_m=\sum_{i=1}^{N}w_{mi}e^{-α_my_iG_m(x_i)}
\] 重复以上步骤(从构造弱分类器开始),直到触发某终止条件。
最后,将获得的所有弱分类器与其权值相乘并相加,得到最终分类器: \[ G(x)=sign(f(x))=sign(\sum^{M}_{m=1}α_mG_m(x)) \]
此外,最后获得的分类器的误差值\(e_m\)有一个上界,其值为: \[ \frac{1}{N}\sum^N_{i=1}I(G(x_i)≠y_i)\le\frac{1}{N}\sum_ie^{-y_if(x_i)}=\prod_m{Z_m} \] 还有一些数学特征详见书上。
参考资料:
- 李航《统计学习方法》
- 知乎上的一篇精彩解说 机器学习算法中GBDT与Adaboost的区别与联系是什么?- Frankenstein
- 推荐blog AdaBoost原理(包含权重详细解释)
GBDT(Gradient Boosting Decision Tree)梯度上升树
Gradient Boosting是对AdaBoost的推广。
- AdaBoost算法中,计算过程没有涉及到凸优化过程,整个过程是通过调整两个权重展开的。
- 而GBDT从侧面用到了梯度上升的概念(恰巧完成了一个梯度下降的操作)。因此相比AdaBoost, Gradient Boosting可以使用更多种类的目标函数。
- GBDT和AdaBoost都结合“从整体到细节”的思想,使每个弱分类器对剩下的细节(即残差或误差量,GBDT是残差)进一步拟合,最后就得到了结果。
- 整理一下思路,GBDT的过程为:首先通过某种拟合方法找到第一个函数(回归树)\(h_1(x)\)(已经通过梯度下降最优化),然后对残差 \[ \sum_iy_i-h_1(x_i) \] 计算并以之为目标函数拟合第二棵回归树。以这种做法递归下去直到达到某种条件即可停止训练。最后的预测函数即 \[ F(X)=\sum_i{h(x_i)} \]
- 注意,对每个弱分类器的优化是独立于GBDT算法的,优化过程参考以往的学习方法进行,如:梯度下降、穷举。
- 可以观察到GBDT的一个重要的特性,也就是梯度出现的地方:用回归树去拟合残差其实就是用回归树去拟合目标方程关于\(F(x_i)\)的梯度。换句话说,就是拟合残差这一个操作恰巧和梯度下降一步是一样的。 证明: 训练过程中,当前的预测函数即 \[
F(X)=\sum_i{h(x_i)}
\] 考虑使用最小二乘代价函数: \[
L=\frac{1}{2}\sum_i(y_i-F(x_i))^2
\] L对上一个弱分类器单个样本点求偏导有: \[
\frac{\partial{L}}{\partial{F(x_i)}}=\frac{\partial\frac{1}{2}\sum_{i}(y_i-F(x_i))^2}{\partial{F(x_i)}}=-(y_i-F(x_i))
\] 而\(y_i-F(x_i)\)是我们要拟合的对象(GBDT中),所以我们拟合的是代价函数对上一个弱分类器的负梯度。这里联想梯度下降的过程:要更新哪个参数,就对哪个参数求导,所以在这里,我们更新的是弱分类器本身(把上一个分类器当作参数)。将拟合后的结果加入到目标函数中也就相当于对上一阶段加入的弱分类器做了梯度下降。
这就是GBDT中的G(梯度)的来源。
XgBoost
- XgBoost是GBDT的改进。 XgBoost对GBDT的代价函数加入了正则化项防止过拟合。如,最小二乘代价函数变形为: \[ L=\frac{1}{2}\sum_i(y_i-F(x_i))^2+\sum_kΩ(f_k) \] 同时,XgBoost使用二阶泰勒展开来代替GBDT中对上一个弱分类器的一阶导数。
XgBoost相关的解释计划在下一篇继续。