ROC、PR和REC曲线、AUC、AOC与肘部方法浅析

机器学习
机器学习-算法

ROC、PR和REC曲线、AUC、AOC与肘部方法浅析

ROC与AUC

ROC与AUC的基本概念

  • 在仅输出概率值的模型中，不能使用准确率、召回率等数值来衡量模型的好坏（除非人为设定了阈值）；这个时候需要一种衡量模型本身好坏而不是衡量阈值好坏，并且能够找到科学的阈值的方法。ROC（receiver operating characteristic）曲线正是这种方法。
  • ROC曲线是用来衡量输出概率值的二分类模型的好坏的一种方法。
  • AUC是ROC曲线与x轴围成的面积大小。

ROC曲线画法

  1. 条件：模型的输出是概率值而不是0和1
  2. 人为设置不同阈值，以FPR（FP/N=FP/(FP+TN)，即误分为1的样例占所有0样例的比例）为横坐标，TPR或召回率（TP/P=TP/(TP+FN)，即正确分类为1的样例占所有1样例的比例）为纵坐标可以绘制出曲线

ROC曲线特点：

1. ROC曲线可以用来判定一个输出概率的模型（需要设定阈值）的好坏 2. ROC曲线越接近左上角，则模型越好 3. ROC曲线的面积（AUC）越接近1，则模型越好 4. ROC曲线的折线段数与样本的数量一致，所以样本越多，ROC曲线越光滑 ROC计算示意 5. 如上图所示，TPR用到的TP和FN同属P列，FPR用到的FP和TN同属N列，所以即使P或N的整体数量发生了改变，也不会影响到另一列。也就是说，即使正例与负例的比例发生了很大变化（样本不平衡），ROC曲线也不会产生大的变化。 6. 综上，ROC适合衡量一个模型本身，与PR相反。

肘部方法

  • 在实际模型的构建时，我们需要确定一个判断结果是否为1的阈值以输出二分类的结果。而阈值的选择是人为的，对模型的预测结果影响很大，所以需要一个科学的方法来确定阈值。
  1. 根据ROC图像的肘部可以确定阈值
  2. 分析： 假设样本平衡，即\(P=N\)，有如下证明：

\[ FPR=\frac{FP}{N}=\frac{FP}{FP+TN} \]

\[ TPR=\frac{TP}{P}=\frac{TP}{TP+FN} \]

\[ \because{P=N} \]

\[ \therefore{ \frac{FPR}{TPR}=\frac{FP}{TP} } \]

要使模型更好，则FP越小越好，TP越大越好；则纵坐标比横坐标的比值越大越好；在比值一定的情况下，若将FP和TP看作同等重要，则纵坐标越大越好（比值不变时，我们希望TP越大越好），所以选择肘部处的阈值最合适。

PR曲线

PR曲线画法

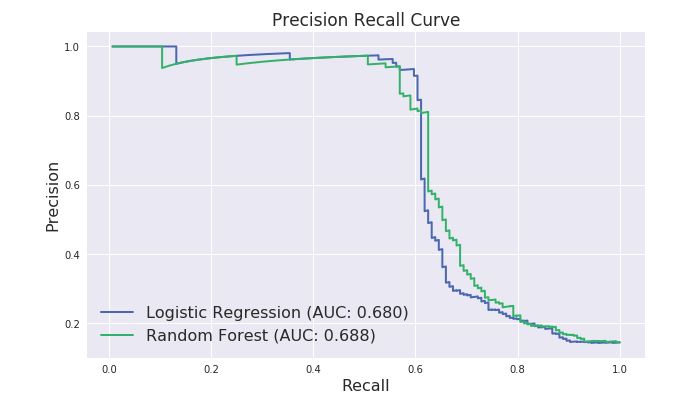
  • 人为设置不同阈值，以召回率recall（TP/P=TP/(TP+FN)），为横坐标，准确率Precision（TP/(TP+FP)）为纵坐标，绘制出PR曲线。
  • PR曲线展示的是Precision vs Recall的曲线，PR曲线与ROC曲线的相同点是都采用了TPR (Recall)，都可以用AUC来衡量分类器的效果。不同点是ROC曲线使用了FPR，而PR曲线使用了Precision，因此PR曲线的两个指标都聚焦于正例。类别不平衡问题中由于主要关心正例，所以在此情况下PR曲线被认为优于ROC曲线。

PR曲线特点

  1. PR曲线可以用来判定一个输出概率的模型（需要设定阈值）的好坏
  2. PR曲线越接近右上角，则模型越好
  3. PR曲线的面积（AUC）越接近1，则模型越好
  4. PR曲线的折线段数与样本的数量一致，所以样本越多，PR曲线越光滑
  5. PR曲线使用了Recall与Precision，因此PR曲线的两个指标都聚焦于正例。
  6. 综上，PR适合衡量一个模型在正样例上的表现，适合处理不平衡问题。

Regression Error Characteristic

简介

  • REC曲线是在ROC曲线的基础下提出的用来衡量回归模型好坏的方法。

作图方法

  • REC曲线的横坐标是回归误差容忍度ε，纵坐标是在容忍度内的“正确分类”的百分比，即若在容忍度内则记为“正确分类”时模型的准确率。通过更改容忍度可绘制出REC曲线。
  • 在容忍度内的定义：
  1. 首先定义一个代价函数，如差值平方、绝对值等。
  2. 若代价函数小于ε，则认定该预测在容忍度内预测正确。

特点

AOC

  • AOC（area-over-the-curve）面积为该模型的不准确率的期望，即随机选择一个阈值时，1与其准确率的期望的差。
  • 其定义为：

\[ E(ε)=\int_{0}^{ε_{m}}p(ε)dε+\int_{ε_{m}}^{+\infty}p(ε)dε \] 即曲线与y=1所围成的面积。

（原论文中的公式如下，个人感觉不太对，在这里也贴出来：）

\[ E(ε)=\int_{0}^{ε_{m}}εp(ε)dε+\int_{ε_{m}}^{+\infty}εp(ε)dε \]

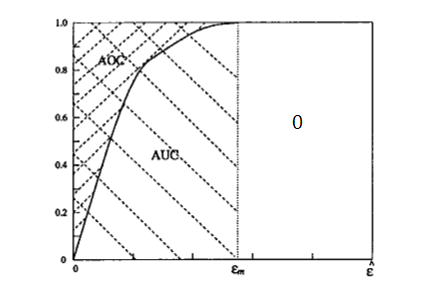
  • 由图像可以得出，AOC只需要计算\(ε_m\)之前的积分就够了。

REC曲线特点：

  1. REC曲线可以用来判定一个输出概率的模型（需要设定阈值）的好坏
  2. REC曲线越接近左上角，则模型越好
  3. AOC越接近0，则模型越好
  4. REC曲线的折线段数与样本的数量一致，所以样本越多，REC曲线越光滑
  5. 由于REC的横纵坐标与样本比例无关，与ROC类似，即使正例与负例的比例发生了很大变化（样本不平衡），REC曲线也不会产生大的变化。
  6. 综上，REC适合衡量一个模型本身。

肘部方法

  • 与ROC类似，REC也有肘部方法可以用来确定合适的ε值，我们希望模型越精细越好，所以ε越小越好；同时我们也希望准确率越大越好。如果将这两个指标等同看待，则有肘部处的ε最好（证明方法跟ROC基本一致）。

参考资料