DeepFool: a simple and accurate method to fool deep neural networks浅读
简介
- Deepfool可做无目标攻击与有目标攻击,无目标攻击时遍历所有类并找到样本变化最小的;有目标攻击则针对该类的超平面进行。
- Deepfool是基于超平面分类思想的一种对抗样本生成方法。众所周知,在二分类问题中,超平面是实现分类的基础 ,那么要改变某个样本 x 的分类,最小的扰动就是将 x 挪到超平面上,这个距离的代价最小。多分类的问题也是类似。
- Deepfool使用该处的切平面与0水平面的交线作为决策边界的近似,所以并不能找到最小的距离(除非分类器为线性)。
- Deepfool的思想是,每次迭代求出该位置的切平面(使用切平面近似代替整个预测函数),然后将该样本点移动到切平面对应的函数值为0的位置。
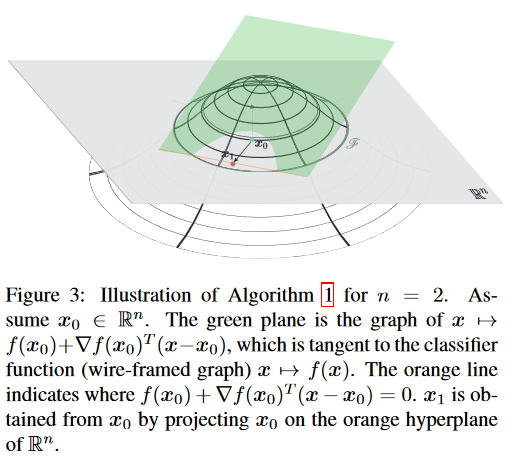
二分类下的公式证明
- deepfool使用的迭代公式为(第i次扰动的计算,注意此时假设样本点处函数值为正,目的是要将其识别为负,即0所对应曲线为决策边界;反之需要修改梯度的方向):
\[ \boldsymbol{r_i}=-\frac{f(\boldsymbol{x_i})}{||\nabla f(\boldsymbol{x_i})||^2_2}\nabla f(\boldsymbol{x_i}) \]
证明
定义以及约定:
\[ 为了便于理解,在三维坐标o-xyz内给出证明,\\其中,x与y对应数据的特征X(该数据有两个特征),z对应f的输出值;\\ f(x, y)→z: 输入为数据,输出为二分类函数的softmax之前一层;\\X_0为数据点,其对应的z(即z_0)有:z_0>0,需要使之小于0而达到攻击效果;\\X_0'为X_0在z=0上的投影\\ f(x)=0为决策边界\\证明过程:\\ 易得曲面f(x, y)-z=0在X_0处的切平面方程:\\ f'_{x_0}(x-x_0)+f'_{y_0}(y-y_0)-(z-z_0)=0\\ 令z=0,得切平面与z=0的交线l:f_{x_0}'(x-x_0)+f_{y_0}'(y-y_0)+z_0=0\\ 化简得l:f'_{x_0}x+f'_{y_0}y-f'_{x_0}x_0-f'_{y_0}y_0+z_0=0\\ 点X_0'到l的距离d为:\\ \frac{|f'_{x_0}x_0+f'_{y_0}y_0-f'_{x_0}x_0-f'_{y_0}y_0+z_0|}{\sqrt{f'^2_{x_0}+f'^2_{y_0}}}=\frac{|z_0|}{\sqrt{f'^2_{x_0}+f'^2_{y_0}}}\\ 又有f(x_0, y_0)=z_0>0 ∴d=\frac{f(x_0, y_0)}{\sqrt{f'^2_{x_0}+f'^2_{y_0}}}\\交线l的法向量为:(f'_{x_0}, f'_{y_0}) \]
整理一下,可以得到结论:
\[ \frac{f(\boldsymbol{x_i})}{||\nabla f(\boldsymbol{x_i})||_2} 为点x_i到决策边界近似直线(近似直线的定义见前文)的距离\\ \frac{\nabla f(\boldsymbol{x_i})}{||\nabla f(\boldsymbol{x_i})||_2} 为单位法向量(也是梯度方向的单位向量)\\ 所以两者相乘再乘-1即将点平移到近似决策边界的向量 \]
多类别
- 由二分类比较容易推广到多分类:
\[ 令h(x)=f_{orig}(x)-f_{t}(x) \]
\[ 其中,f_{orig}是原类别的对应函数;f_{t}是目标类别的对应函数 \]
\[ 若攻击成功,则f_{t}(x_i)所对softmax大于f_{orig}(x_i)所对softmax \]
\[ 则f_{t}(x_i)>f_{orig}(x_i) \]
\[ ∴ 当h(x)<=0时达到攻击目的,此时即转化为二分类一样的情况 \]
- 需要注意的是,多分类一次迭代时会计算所有其他非原类的变化距离,并采用变化距离最小的类作为此步的动作。
- 此外,由于deepfool所求距离只能将点移动到决策边界上,实际移动时需要多移动一点以越过边界。
- 多分类deepfool的伪代码如下:

- 论文同时指出,伪代码中使用\(l_2\)范数作为扰动大小的判断依据,但是只要将10行和11行的2换成p,就可以使用任意范数作为扰动依据。
其他结论
- 论文提出了使用deepfool方法得到的扰动和数据点X的第二范数的比值作为衡量各模型鲁棒性的标准(该数值越大,鲁棒性越强),并给出了对LeNet等模型的测评结果。
- 论文使用deepfool与fgsm对比,deepfool得到的扰动要远小于fgsm。
- 论文指出,DF可以在3次迭代之内就找出对抗样本,其效率较其他方法更高。
- 论文还使用deepfool和fgsm对不同模型进行对抗训练,并使用deepfool对其鲁棒性进行评估,得到了deepfool对抗训练效果更好、还能够略微提高原模型的准确性(fgsm则会降低准确性)。fgsm的对抗训练反而使鲁棒性降低了;但是增大扰动的大小再进行对抗训练时,deepfool也使鲁棒性降低了。得出如果扰动较大,对抗训练反而会使鲁棒性降低(同时给出解释:当扰动过大时,数据被“真正地”改为另一类别的数据)。
- df鲁棒性能够衡量测试集的准确率,(脑洞)可能可以作为指导finetune提前截止的依据(提前终止这个操作并没有什么依据);同时,在对抗训练时可以调缓学习率。
经过小实验得到的一些结论
代码
- 参考了LTS4,经过压缩修正的代码主要流程如下:
|
|
注意事项
- 由于求梯度的灵敏度问题,deepfool使用
softmax之前的一层作为输入,否则效果很差。
改变overshoot值得到生成样本
- 比较有趣的是,通过加大overshoot值,得到的图片人工也能识别成另一种图像,这与GAN得到的生成结果非常类似:
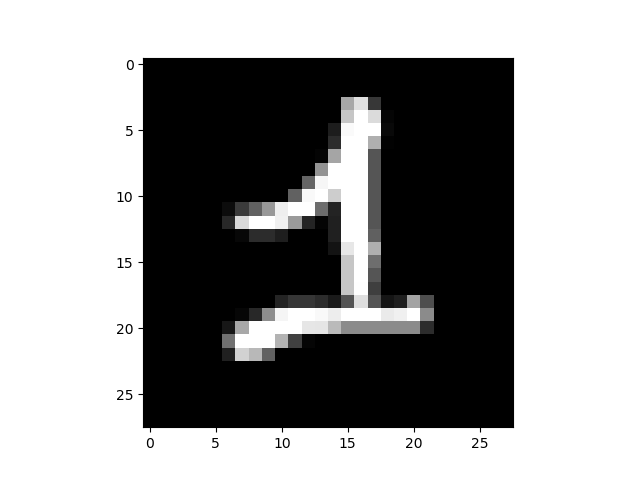
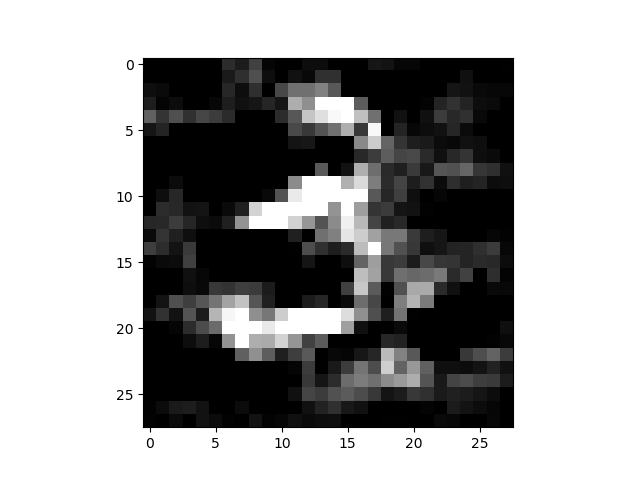
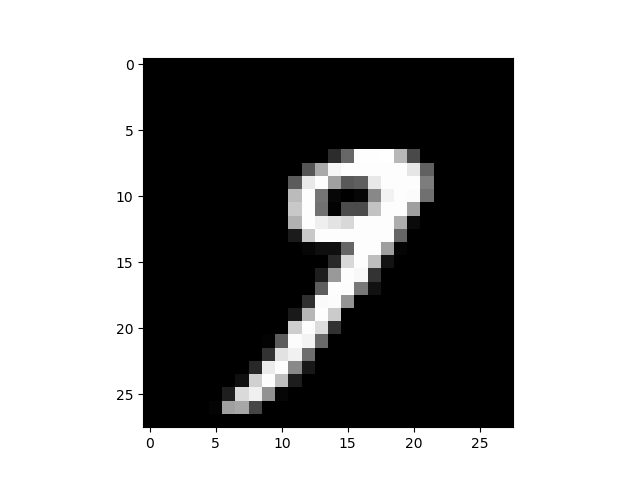
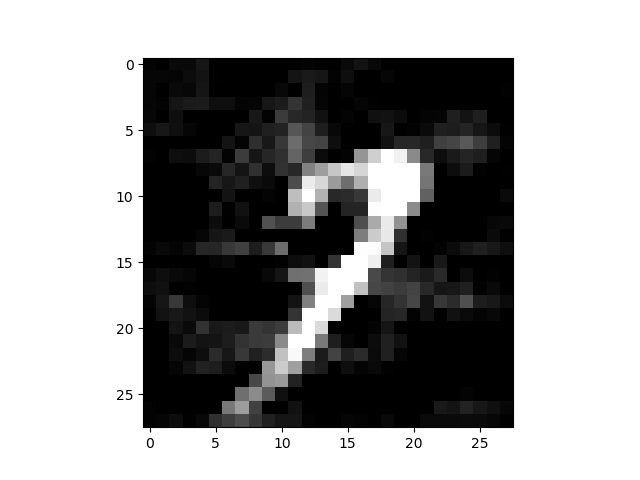
总结
- 论文提出了deepfool对抗攻击算法,该算法效果超越了IFGSM等算法。
- 论文提出了基于DF对模型抵抗扰动的鲁棒性进行评估的方法。
- 论文指出DF在加大overshoot值时,真正地产生了其他类别的数据。
- 论文指出DF的对抗训练可以增大模型的准确率和鲁棒性。
参考资料
- Moosavi-Dezfooli S M, Fawzi A, Frossard P. Deepfool: a simple and accurate method to fool deep neural networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition.2016: 2574-2582.
